KnightL on a Chessboard(HackerRank) - BFS

Problem Link: KnightL on a Chessboard

KnightL is a chess piece that moves in an L shape. We define the possible moves of KnightL(a,b) as any movement from some position (x1,y1) to some (x2,y2) to some satisfying either of the following:

* x2 = x1 ± and a, y2 = y1 ± and b or
* x2 = x1 ± +b and , or y2 = y1 ± a

Note that (a,b) and (b,a) allow for the same exact set of movements. For example, the diagram below depicts the possible locations that KinightL(1,2) or KnightL(2,1) can move to from its current location at the center of 5 x 5 a chessboard:

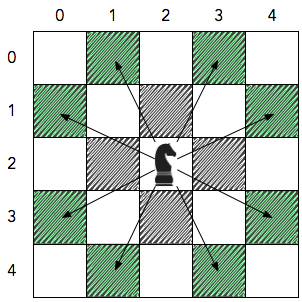
Observe that for each possible movement, the Knight moves 2 units in one direction (i.e., horizontal or vertical) and 1 unit in the perpendicular direction.

Given the value of n for an n x n chessboard, answer the following question for each (a,b) pair where 1 <= a, b < n:

What is the minimum number of moves it takes for KnightL(a, b) to get from position (0, 0) to position (n-1, n-1) ? If it’s not possible for the Knight to reach that destination, the answer is -1 instead.

Then print the answer for each KnightL according to the Output Format specified below.

Input Format

A single integer denoting .

Constraints

5 ≤ n ≤ 25

Output Format

Print exactly n-1 lines of output in which each line i (where 1 ≤ i < n ) n-1 contains space-separated integers describing the minimum number of moves KnightL(i, j) must make for each respective j (where 1 ≤ i < n ). If some KnightL(i, j) cannot reach position (n-1, n-1), print -1 instead.

For example, if n=3 we organize the answers for all the (i, j) pairs in our output like this:

(1,1) (1,2)
(2,1) (2,2)

Sample Input 0

Sample Output 0

Explanation 0

The diagram below depicts possible minimal paths for

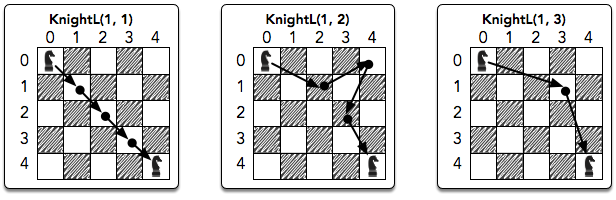
One minimal path for

(0,0) -> (1,4) -> (2,0) -> (3,4) -> (4,0) -> (0,1) ->(4,2) -> (0,3) -> (4,4)

We then print 4 4 2 8 as our first line of output because KnightL(1,1) took 4 moves, KnightL(1,2) took 4 moves, KnightL(1,3) took 8 moves.

In some of the later rows of output, it’s impossible for KnightL(i,j) reach position (4,4). For example, KnightL(3,3) can only move back and forth between (0,0) and (3,3) so it will never reach (4,4).

Solution (C++)

bool isvalid(int x, int y, int n) {
    if (x < 1 || y < 1 || x > n || y > n)
    {
        return false;
    } 
    return true;
}

int bfs(int a, int b, int n) {
    int dx[8] = { -a, -a, -b, b, -b, b, a, a };
    int dy[8] = { b, -b, -a, -a, a, a, b, -b };
    int dist[30][30];
    memset(dist, -1, sizeof(dist));
    bool isvisited[30][30] = { false };
    dist[1][1] = 0;
    isvisited[1][1] = true;
    queue<pair<int, int>> dq;
    dq.push(make_pair(1, 1));
    while (dq.size()) {
        int currX = dq.front().first;
        int currY = dq.front().second;
        dq.pop();
        for (int i = 0; i < 8; i++) {
            int newX = currX + dx[i];
            int newY = currY + dy[i];
            if (isvalid(newX, newY, n) && !isvisited[newX][newY]) {
                isvisited[newX][newY] = true;
                dist[newX][newY] = dist[currX][currY] + 1;
                dq.push(make_pair(newX, newY));
            }
        }
    }
    return dist[n][n];
}

vector<vector<int>>knightlOnAChessboard(int n) {
    vector<vector<int>> result;
    for (int i = 1; i < n; i++) {
        vector<int> temp;
        for (int j = 1; j < n; j++) {
            int res = bfs(i, j, n);
            temp.push_back(res);
        }
        result.push_back(temp);
    }
    return result;
}

BFS 複習筆記

使用 BFS 目的？找到起點至終點的最短距離
為何 BFS 可以得到最小步數？在進入下一層之前，會遍歷此層，若到達終點則為答案
BFS 基本資料結構為 queue，將周圍即將遍歷的點加入

queue<pair<int, int>> dq; //以此題為例，將 pair 型態放進 queue

檢查下個拜訪點是否合法、是否拜訪過，再加入 queue，做為下一個需要拜訪且向下延伸的對象

if (isvalid(newX, newY, n) && !isvisited[newX][newY]) {
    isvisited[newX][newY] = true; //拜訪紀錄
    dist[newX][newY] = dist[currX][currY] + 1; //更新步數
    dq.push(make_pair(newX, newY)); //放入貯列做下一層延伸
}

KnightL on a Chessboard(HackerRank) – BFS